|
That little picture shown above is my avatar on multiple discussion boards about chainmail. I’m a self-proclaimed aspect ratio zealot. I think that everyone else should be too. Some have asked why I feel this way, and this is my answer.
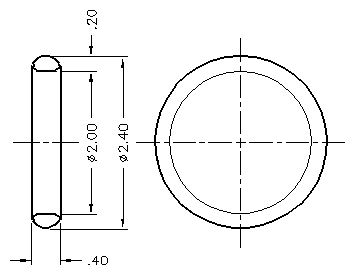
What is the Aspect Ratio?What is an aspect ratio anyway? Isn’t it something to do with the size of a TV? In normal, everyday use, yes, it is. It is the width-to-height ratio of a film or television image. 4:3 is the aspect ratio for normal TV, and 16:9 is the normal ratio for film or HDTV. For a full in-depth article about TV/wide screen aspect ratios, check out http://www.thedigitalbits.com/articles/anamorphic/aspectratios/widescreenorama.html. In chainmail circles, the aspect ratio is the ratio between the inner diameter of a ring and the diameter of the wire from which it is made, or AR = Ring I.D. / Wire Dia. Each chainmail weave requires rings of some certain size to work. After learning a few weaves in 14 or 16 ga. wire, you might become interested in trying out your newfound knowledge in wire of a different size. To figure out your new ring I.D, use the following equation: New Ring I.D. = New Wire Dia. x AR Inch, millimeter or fathom, it doesn’t matter what unit you’re using; you will always get the ring I.D. in the same unit as your wire diameter. Who came up with the equation?I don’t know. Why is this the equation? Why not the Wire Dia. / Ring O.D. (outer diameter) or something else?I don’t know this one either, but I do have a pretty good idea, as this is same equation that I would have come up with if there was not one already. The purpose of coming up with the ratio was to have a unitless number that could be used to identify the ring. This way, the number would work with any measurement system, be it metric, English or whatever you use in your own world. When making a ring, you generally know 2 things: the mandrel diameter and the wire diameter. Therefore, it makes sense to use what you know. So, the basic equation had 2 choices: (a) AR = mandrel diameter / wire diameter, or (b) AR = wire diameter / mandrel diameter Normally, in ratios, your small number is greater than or equal to 1, so it makes sense to choose the equation that gives a number greater than 1 -- Equation (a). You may have noticed that Equation (a) lists "Mandrel Diameter" in the equation, while the equation at the very beginning lists "Ring I.D." Aren’t these the same? Short answer, no. Long answer, keep on reading. Mandrel diameter vs. Ring diameter: What’s the difference?In a word, springback. According to www.dictionary.com, springback refers to: "a flying back; the resilience of a body recovering its former state by elasticity; as, the spring of a bow", or, in our case, a coil of wire. When winding wire on a mandrel into a coil, the coil unwinds a little bit when tension on the wire is released. This results in the rings having a slightly larger ring I.D. than originally anticipated. The type of material used, tension on the wire while coiling and speed of coiling are some of the factors involved in springback, making it difficult to come up with a common number that everyone can use. Material seems to have the greatest impact on springback. The following 2 definitions come from David Austin (aka Odin): IAR = ideal aspect ratio; ideally, the inside diameter of a ring is equivalent to the size of the mandrel. AAR = actual aspect ratio; this is determined if you take into account springback from coiling. To me, the only AR to use is the actual AR, as this is the only one that is consistent for all materials, provided that they have the same cross-section. We will discuss cross-sections and their effects on aspect ratio a little bit later. Unfortunately, most maillers seem to work with the IAR, because they don’t have the capabilities to measure the ring I.D. or wire diameter so they can obtain the AAR. What’s the best way to measure a ring I.D.?Get yourself a set of dial or digital calipers. On www.mcmaster.com, you can order a 4" set of "Economy Dial Calipers" for $20.91 USD. With a little searching, you should definitely be able to find them cheaper. Close at least 10 rings, and take I.D. AND wire diameter measurements of all the rings. Calculate the average of your I.D.’s, and wire diameters and use the averages in the equation. Just for grins, let’s calculate those "ideal" and "actual" aspect ratios for a 16 ga. x 1/4 I.D. (.265 actual) galvy. IAR = .250 / .063 = 4.00 AAR = .265 / .063 = 4.20 That’s a 5% difference for a material that doesn’t really spring that much. It’s only going to get worse as you move to materials like stainless, or for the masochists out there, spring stainless. Do I really need to measure the wire diameter? It says the wire gauge and/or diameter right on the spool!You should. Just because it says so doesn’t mean it’s true. In the words of Bob Dylan, "If you need somebody you can trust, trust yourself." According to Central Steel & Wire Supply Data Book, the tolerance for wire is ±1%. Not all wire manufacturers have that tight of a tolerance, and you’ll need to know what your rings really are, especially if you are a micromailler. A difference of .002 inches (that’s .05 mm for you metric folk) may not seem like much, but if it was in a 24 ga. wire (.020 inches, let’s say .018 actual), that could make a difference on your .080 I.D. (measured, not mandrel).Again, just for grins, let’s calculate the aspect ratio using the manufacturer’s size and your measured size. IAR = .080 / .020 = 4.00 AAR = .080 / .018 = 4.44 That’s an 11% difference! Of course, you were actually changing the wire diameter by 10%. Small changes are large when you are using small wire! Now, you might think I’m just trying to scare you, but I have had wire that was .006 off before (works out to 14%), and that was enough to change what weaves I could do with the wire. Why do you think I’m an aspect ratio zealot? What aspect ratio are shower rings? Or, how do cross-sections affect aspect ratios?Well, this is where things get a little tricky. For BlueBuddha’s shower rings (basic blueprint shown below), the correct answer is somewhere between 5 and 10, if you’re comparing them to round rings.
How do I get the answer of 5-10? Well, 2.00 (ring I.D.) / .40 (the ring width) = 5, and 2.00 (ring I.D.) / .20 (the ring cross-section height) = 10. On wire with a circular cross-section, the ring width is equal to the ring cross-section height, so the numbers are the same. Because the shower ring has a different cross-section than the rings we normally use, our numbers do not necessarily correlate. For weaves that require an aspect ratio of 5 or below, such as Half Persian 4-1 or Euro 4-1, the shower ring would work fine. For a weave like Half Persian 5-1 chain (for which I like an AR of 7.1), I couldn’t tell you one way or the other if it was going to work without trying it. Different weaves will be affected differently, depending on where the rings contact each other. I hope this answers your questions about aspect ratios. If you're still confused, you might want to check out the Aspect Ratio article by Theresa Olin (aka La Vacacita) or the article "What is the Aspect Ratio? (And why is it important?)" by Spider. Questions or comments? Email me at mailler@zlosk.com. |